2613. Maximum sum

Given a table with integers of size n ⋅ n. Find in it the rectangle with maximum sum. For example, in the table

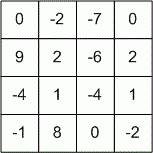
the rectangle with maximum sum is

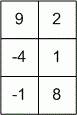
Sum of its elements equals to 15.

Input. First number n (n ≤ 500) is the size of the table. Then n² integers are given that describes the table. It is known that all numbers are integers in the range [-127, 127]. It is known that the table contains at least one nonnegative integer.

Output. Print the maximum sum in rectangle.

Sample input	Sample output
4 0 -2 -7 0 9 2 -6 2 -4 1 -4 1 -1 8 0 -2	15

SOLUTION

dynamic programming

Algorithm analysis

Let the input table be stored in the array table, with the top left cell stored in table[1][1].

Recompute its elements in such a way that _table[i][j] = . That is, _table[i][j] contains the sum of the elements of table[i][j] that are in the same column, but not below the element (i, j).

Now the sum of the numbers s of any rectangle with the upper left corner (i₁, j₁) and the lower right corner (i₂, j₂) can be calculated in linear time:

s =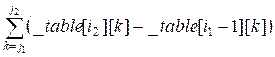

On the left there is an input table, on the right there is a transformed one.

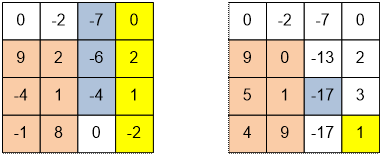
For example

_table[3][3] = table[1][3] + table[2][3] + table[3][3] = -7 – 6 – 4 = -17,

_table[4][4] = table[1][4] + table[2][4] + table[3][4] + table[4][4] =

0 + 2 + 1 – 2 = 1

The sum of the numbers in the rectangle (2, 1) – (4, 2) is equal to

=

=

(4 – 0) + (9 – (-2)) = 15

Let’s fix two lines i and j. Now let’s find the size of the maximum rectangle that touches line i from above and line j from below (both lines inclusive). Construct a sequence A of numbers a₁, a₂, …, a_n, for which a_k = _table[j][k] – _table[i – 1][k]. It remains to find a subsequence of consecutive numbers in sequence A that has the maximum possible sum. This is a well-known one-dimensional problem that can be solved through partial sums s_k = a₁ + … + a_k (as soon as the partial sum becomes less than 0, we reset it to zero and continue to count).

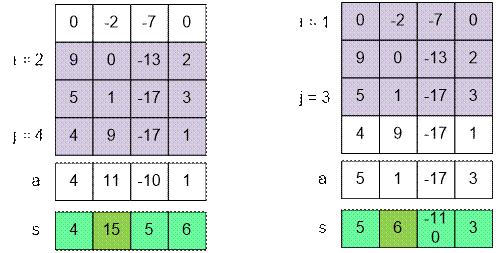
The maximum rectangle between:

· rows 2 and 4 has sum 15;

· rows 1 and 3 has sum 6;

Algorithm realization

Declare an array.

#define MAX 502

int table[MAX][MAX];

Read the input data.

scanf("%d", &n);

memset(table,0,sizeof(table));

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

scanf("%d",&table[i][j]);

Recompute the array table.

for (j = 1; j <= n; j++)

for (i = 1; i <= n; i++)

table[i][j] = table[i - 1][j] + table[i][j];

We look for a rectangle with the maximum sum. Iterate over rows i and j (1 ≤ i ≤ j ≤ n). Next, calculate the partial sums s_k and solve the one-dimensional problem.

for (i = 1; i <= n; i++)

for (j = i; j <= n; j++)

{

t = 0;

for (k = 1; k <= n; k++)

{

t += table[j][k] - table[i-1][k];

if (t < 0) t = 0;

if (t > max) max = t;

}

}

Print the sum in the maximum rectangle.

printf("%d\n", max);